SELECT LANGUAGE: ENGLISH | ITALIANO
NEXXUS
NEXXUS PROCESSOR vs CONVENTIONAL SCREW EXTRUDERS:
PROCESSING QUALITY and QUALITY DISTRIBUTION

The processing quality distribution in a conventional screw extruder is generally very broad as it depends on the ratio of the flow rate parallel to the flight Qa vs flow rate normal to the flight Qc. The parallel flow rate produces the familiar delivery rate, thus out of the extruder, while the normal flow rate, also termed circumferential flow rate, doesn’t produce any delivery flow but just liquid deformation as it passes through the flight/s clearance/s. This circumferential flow is the core dispersion in screw extruders as it generates the powerful elongational flow components which are the most suitable to deform the liquid.

An example of the deformation undergone by the material during its circumferential flow is given by the elongational-dispersive stresses typically occurring along with circumferential convergent channels, between flight and barrel. One more example of the circumferential deformation is given by the thin lamination of the liquid over the barrel wall typically occurring in the degassing section of extruders.
It is intuitive that not all liquid particles spend the same time when flowing between the entrance and the exit of the extruder, for the reason that some particles make more circumferential passages than others. Therefore an observer fixed at the extruder exit will see the liquid particles leaving in a different sequential order as compared with the sequential order at the entrance. These unequal circumferential passages give rise to different residence time histories and, of course, different deformational histories. The consequence is that the processing quality distribution gets quite broad.
Just to make an example, if we number all entering particles sequentially from 0 to 23, an observer fixed at the exit will see at sequential time instants, for example, t0, t1…t5 etc. different sequences as compared with the entrance sequences.
If we select, for example, quaternary sets we’ll have:
TAV. 1
It is obvious that liquid particles 1 and 2 appearing in the 1st exit sequence have spent, into the extruder, more time than, for example, particle 21 and therefore have undergone longer dispersive deformation and thermal history, than the particle 21 etc.
The flow nature of a liquid conveyed down to a screw channel is intrinsically bi-dimensional. This happens as the helical channel guides the material to flow in part parallel to the flight and in part normal to the flight. Obviously a substantial circumferential flow requires a significant flight clearance to exist, otherwise no liquid can flow over. Significant flight clearances are designed, for example, in co-rotating twin screw extruders or in special mixing sections of single screw extruders.
Bidirectional flow down the screw
channel in a single screw extruder 		Bidirectional flow in the mixing section
of a single screw extruder		 Bidirectional flow in the kneading section
of a corotating twin screw extruder

The circumferential flow is highly desired in dispersive mixing zones where the melt needs to be deformed during circumferential rounds. When circumferential flow is required, in a screw extruder, the dispersive mixing quality of the compound depends closely not only on the convergent path geometry (suitable to develop elongational flow components) but also on the ratio λ of the circumferential flow rate Qc to the net axial, delivery flow rate Qa. If the circumferential flow rate is very small (it happens when the flight clearance approaches to zero), then also the λ ratio drops nearly to zero and the “circumferential” deformation doesn’t take place at all. This situation usually occurs in the pumping zone of single screw extruders where the flight clearance is kept to a minimum to enhance pressurization.
Viceversa when a circumferential flow is desired, the flight-barrel gap is designed with values >>0. A flight clearance (h) >>0 in combination with a sufficiently long mixing section (L) and adequate screw speed (U) are the base for producing a substantial circumferential flow rate(Qc=U*L*h). Depending on h, L and U the λ ratio of the circumferential flow rate to the delivery flow rate may be lower, equal or larger than unity (λ<1, λ=1, λ>1). As much as λ ratio increases from 0 to >>1, the dispersion efficiency of the extruder increases but the quality distribution gets broader.

   
Zehev Tadmor e Manas-Ica Zloczower developed a statistical function (NPD-Number of Passages Distribution Function) able to predict the density passages probability for a liquid particles population vs λ, assuming the liquid to be ideally homogenized after each passage (rif.1):
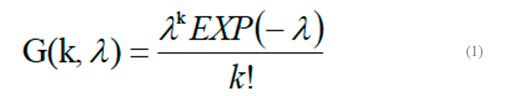  Rif. 1 I. Manas-Zloczower and Z. Tadmor, “The Distribution of Number of Passages over the Flights in Single Screw Melt Extruders”, Adv.Plast.Technol.,3,213, (1983)
   
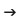In eq. 1 k refers to the probable passage number of all different liquid population fractions. The equation states that the circumferential flow rate must be 4,6 times greater than the axial delivery rate (λ=4,6), to achieve the statistical confidence that all liquid is passed at least 1 time across the flight.
   
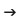Many experimental verifications of NPD theory teach that a λ=4,6 is not sufficient to grant one physical passage for all particles. Moreover in some cases λ=4,6 value has to increase further when more than just one flight passage is needed to meet a certain dispersion level. In many practical cases the critical λ value must rise up to 10 or more.
   
Since the screw speed cannot be increased arbitrarily and not even the flight clearance can be arbitrarily large (to meet the elongational rules), the only screw parameter which can be freely adjusted to get the prescribed λ value, is the dispersive screw length. Unfortunately, as said, by making longer screw section, the dispersive quality of the compound gets broader and the thermal degradation risks more likely to occur.
   
Some NPD curves are sketched below, at different λ values, in all being k ranging between 0 and 2λ, (2λ selection is useful to get a symmetric belt shaped curve). The reported curves show the quite broad quality distribution, for any l condition.
NPD curves for some values λ=5,10,15
and 20-and integer k values ranging between 0 and 2λ.
   
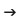For λ= 5, 10, 15 and 20, most material passes through flights 1, 5, 9 and 14 times, respectively. It is evident the limitation sourcing from a high λ value. To increase λ the only practical way (for given screw diameter and speed and flight gap), is to extend axially the mixing section but doing so, all mixing energy, average residence time and machinery investment increase. As anticipated, if the application doesn’t require more than one circumferential passage for all liquid particles, then λ must be at least 4,6. It means, for example, that the circumferential flow rate needs to be at least 460 Kg/h, if the net axial delivery rate is 100 kg/h. But if a given application requires minimum 5 circumferential passages, then λ must be 10 and Qc must be1000 Kg/h etc.
   
To synthesize the above concepts we can say: a) if λ approaches to zero there is no circumferential passage and not even circumferential deformation. b) if λ is sufficiently high as to grant the required minimum number of circumferential passages then the dispersive quality distribution will be fatally and undesirably broad, introducing in the scenario a real risk of thermal degradation.
   
The above arguments apply particularly to the basic processing steps where a narrow quality distribution is desired. These processing steps are first melting, dispersive mixing and degassing.
   
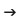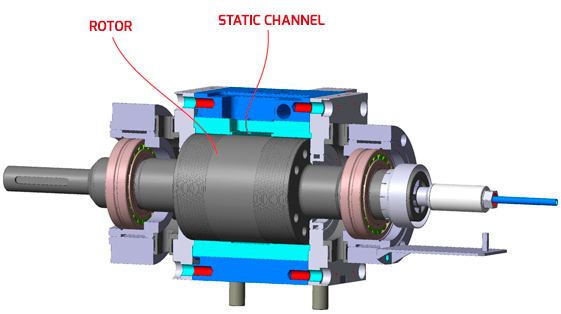
The situation is fairly better with Nexxus Channel processor, where the flow is rigorously mono-dimensional, along the annular circumference of the flow channel.
 
The flow path for the liquid particles population in Nexxus is always the same, for a given model, and corresponds to about 2/3 rotor circumference. It happens with any bush geometry whether the path is simply tapered or also patterned.
   
In case of Nexxus is not necessary to invoke the statistical probability to predict the melt quality distribution, as:
 
  • The residence time of all individual particles is materially identical and approaches to the mean residence time (Rt(x)→Rtav) where x is any particle of the population).
  • The above statement holds for any type of process whether melting, distributive mixing, dispersive mixing and degassing for standard as well as for reactive compounding.
   
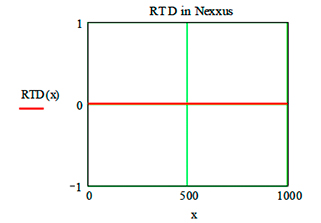
For the above reasons the quality distribution curve in Nexxus gets a straight line parallel to the abscissa (eq. 2). In few words all liquid particles show the same residence time, the same deformational history, the same distributive splitting and recombination flow etc. This is also the ideal condition to maximize the compound quality able to grant an infinite repeatability, under the same operative variables.
   
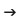Below we show the distribution curve corresponding to the classical normal residence time distribution in Nexxus mixing chamber. The equation of the curve is:
 
Setting the mean value µ =0 and the standard deviation σ very close to 0, for any liquid particle number (say 1000 ) we’ll get:
 
TAV. 2
Repeating, for Nexxus, the flow sequence simulation, sketched above for a screw section, the observer fixed at Nexxus dicharge port, will see leaving the quaternary sequences, numbered from 0 to 23 in the same entrance order:
In conclusion RTD as well as the processing quality distribution approach to ZERO!!

This is a result that simply cannot be reproduced in any existing continuous screw mixer
www.nexxuschannel.it @ 2014 Nexxus Channel All rights reserved / P.Iva 03001710122 / Design and develop: Swingcom.it